문제
하나 이상의 연속된 소수의 합으로 나타낼 수 있는 자연수들이 있다. 몇 가지 자연수의 예를 들어 보면 다음과 같다.
- 3 : 3 (한 가지)
- 41 : 2+3+5+7+11+13 = 11+13+17 = 41 (세 가지)
- 53 : 5+7+11+13+17 = 53 (두 가지)
하지만 연속된 소수의 합으로 나타낼 수 없는 자연수들도 있는데, 20이 그 예이다. 7+13을 계산하면 20이 되기는 하나 7과 13이 연속이 아니기에 적합한 표현이 아니다. 또한 한 소수는 반드시 한 번만 덧셈에 사용될 수 있기 때문에, 3+5+5+7과 같은 표현도 적합하지 않다.
자연수가 주어졌을 때, 이 자연수를 연속된 소수의 합으로 나타낼 수 있는 경우의 수를 구하는 프로그램을 작성하시오.
입력
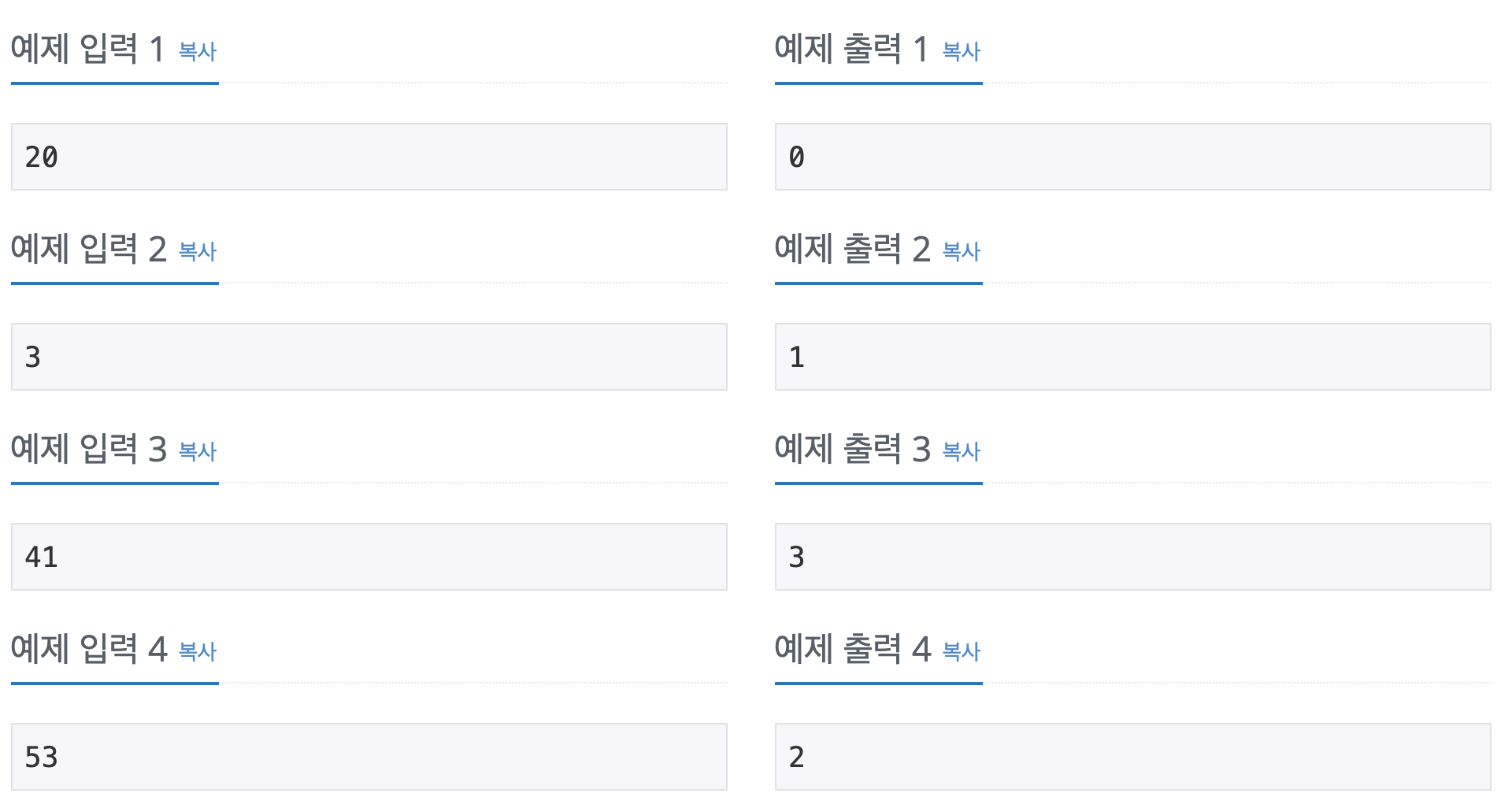
첫째 줄에 자연수 N이 주어진다. (1 ≤ N ≤ 4,000,000)
출력
첫째 줄에 자연수 N을 연속된 소수의 합으로 나타낼 수 있는 경우의 수를 출력한다.
풀이 (에라토스테네스의 체 , 투 포인터)
이 문제는 에라토스테네스의 체와 투 포인터 알고리즘을 함께 사용하면 풀면 된다.
에라토스테네스의 체는 소수를 구하는 알고리즘으로 간단히 설명하자면 어떤 수를 확인하고 나서 그것의 제곱부터 그 수씩 넘어가면서 검사 항목에서 제외시키는 것이다. 예를 들어서 2를 검사하고 나서 2*2부터 2씩 4,6,8,10....씩 검사항목에서 제외하고 3은 9부터 9,12,15..씩 검사에서 제외시켜서 소수를 체크하는데 시간을 줄여준다.
# 에라토스테네스의 체
primeList = []
array = [False, False] + [True] * (N - 1)
for i in range(2, N + 1):
if array[i]:
primeList.append(i)
for j in range(i * i, N + 1, i):
array[j] = False투 포인터는 특정한 합을 가지는 연속된 수열문제를 푸는데 사용되며 연속되는 합들의 부분합을 체크하는데 사용된다.
# 투 포인터
interval_sum = 0
end = 0
count = 0
start = 0
while True:
if interval_sum >= N:
if interval_sum == N:
count += 1
interval_sum -= primeList[start]
start += 1
elif end == len(primeList):
break
else:
interval_sum += primeList[end]
end += 1
이것을 합치는것이 최종 코드이다.
# 1644 소수의 연속합
# Math 소수
# 투 포인터
import sys
input = sys.stdin.readline
N = int(input())
primeList = []
array = [False, False] + [True] * (N - 1)
for i in range(2, N + 1):
if array[i]:
primeList.append(i)
for j in range(i * i, N + 1, i):
array[j] = False
interval_sum = 0
end = 0
count = 0
start = 0
while True:
if interval_sum >= N:
if interval_sum == N:
count += 1
interval_sum -= primeList[start]
start += 1
elif end == len(primeList):
break
else:
interval_sum += primeList[end]
end += 1
print(count)
배운점
처음에는 DFS로 backtracking을 하면서 풀었는데 N이 400만인걸 생각을 안하고 풀어서 시간 초과가 떴었다... N을 고려하지 않은채 문제에 접근했었고 테스트 케이스는 통과했지만 결과적으로는 시간초과였다.
DFS 말고 연속합을 어떻게 빠르게 구할 수 있을까 찾아보게 되었고 투 포인터라는 것을 알게 되었다.
아직까지 시간 복잡도를 생각하면서 푸는것은 어색하지만 그래도 이렇게 하나씩 알아가게 되어 다행이다!!
'Algorithm(알고리즘) > BOJ(백준) 문제풀이' 카테고리의 다른 글
| 백준 2667번 파이썬 | 단지번호붙이기 (DFS 연결노선 찾기문제) (0) | 2020.10.31 |
|---|---|
| 백준 1260번 파이썬 | DFS와 BFS (0) | 2020.10.30 |
| 백준 9095번 파이썬 | 1, 2, 3 더하기 (0) | 2020.10.27 |
| 백준 13305번 파이썬 | 주유소 (0) | 2020.10.26 |
| 백준 2138번 파이썬 | 전구와 스위치 (0) | 2020.10.26 |



